Recordamos que existen tres dimensiones en el espacio (altura, anchura y profundidad, relacionados con los tres ejes de coordenadas x, y, z, aunque normalmente usemos solo los ejes x e y).
1 dimensión → Medir distancias es medir una dimensión del espacio.
2 dimensiones → Medir el área o superficie de una figura plana, será medir dos dimensiones del espacio, por ejemplo en un rectángulo, la altura y anchura.
3 dimensiones → Medir un volumen será medir las tres dimensiones del espacio.
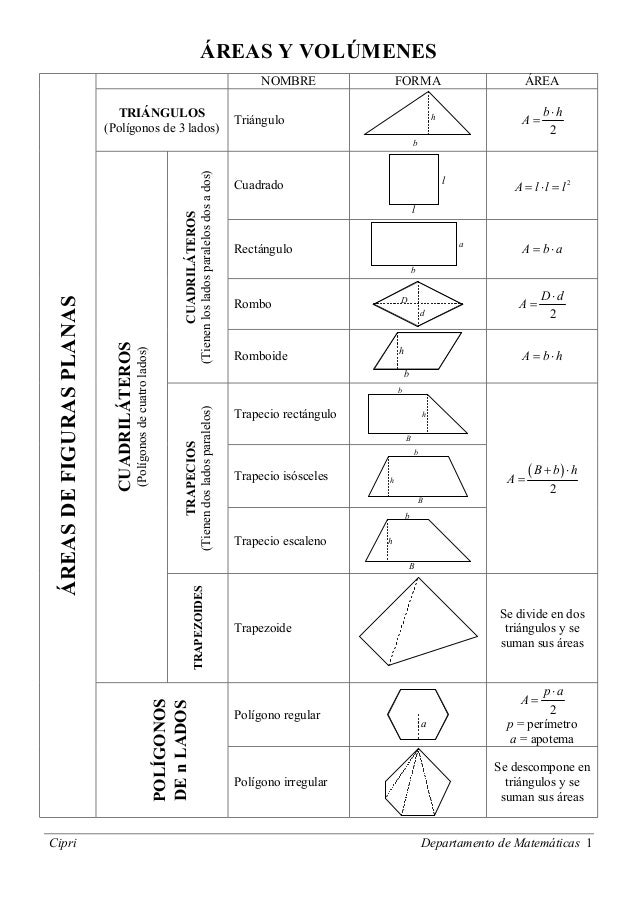
Se puede medir la superficie de una figura con volumen, en el caso de un cubo sería sumar la superficie de las 6 caras que lo forman.
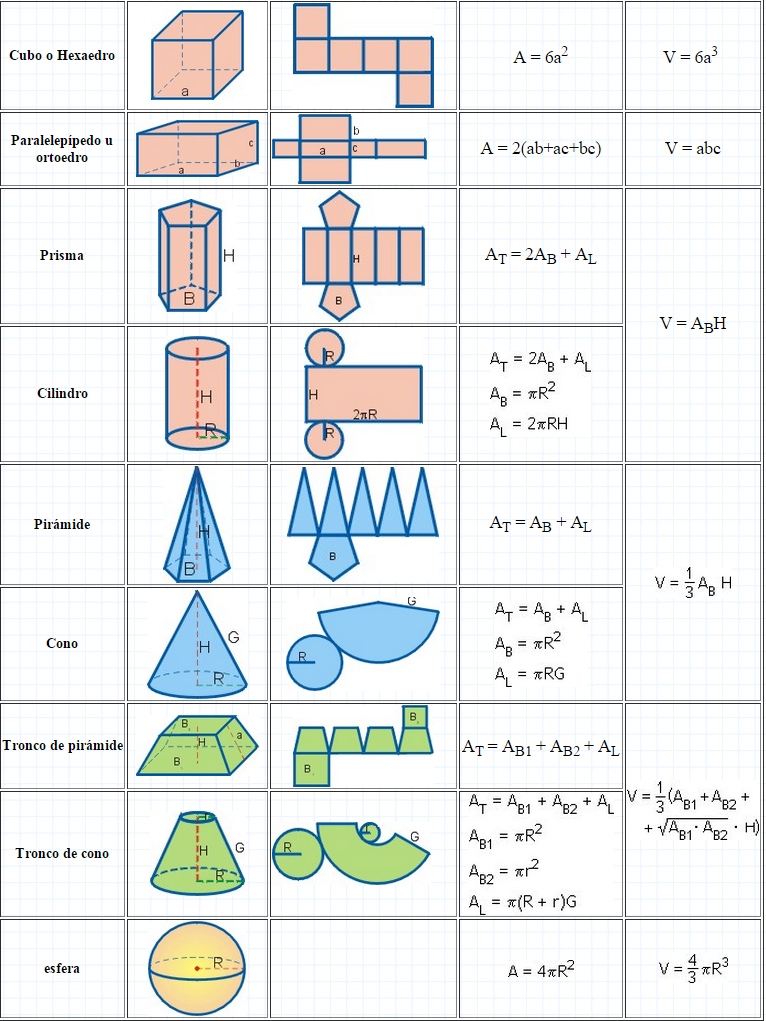
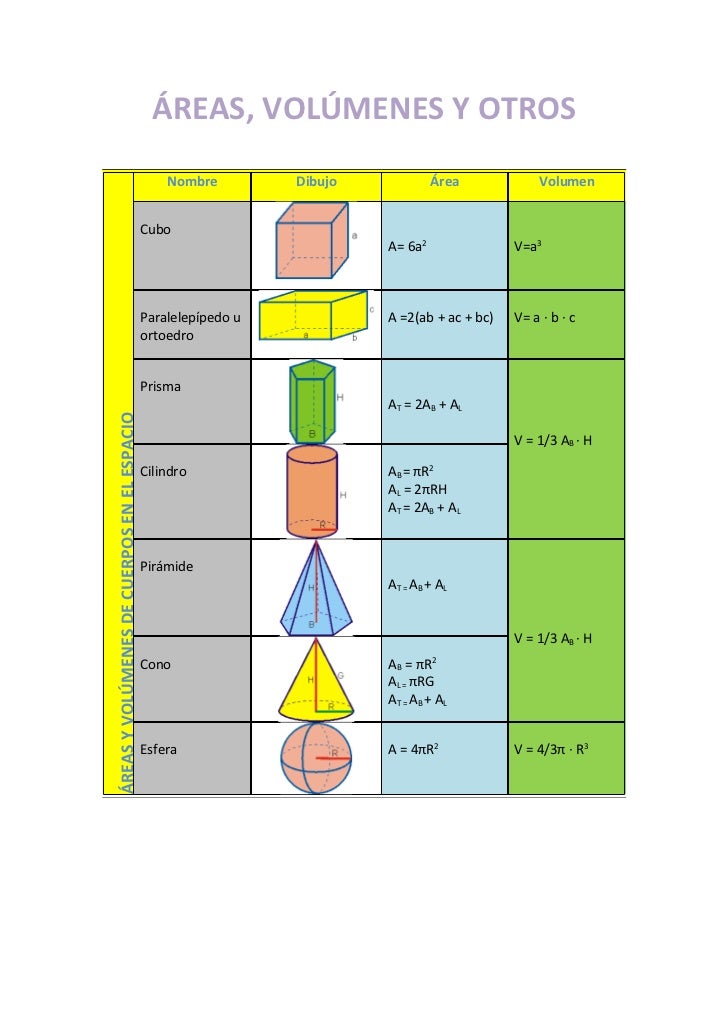
Áreas de polígonos
actividad 2 pag 153
ResponderEliminartriangulo: 180(3-2)/3=180/3= 60
cuadrado: 180(4-2)/4=90
Página 161, ejercicio 37
ResponderEliminarA=3.14x(2.5)elevado a 2=19,63 cm2
Soy Alejandro voy a corregir el ejercicio 9.
ResponderEliminar135= 180(n-2) / n -> 135 n= 180 n - 360 -> 360= 180n-135n -> 45n= 360 -> n=8
Es un octógono
A) lado es igual a raíz cuadrada de la hipotenusa al cuadrado menos el cateto al cuadrado que es igual a la raíz de 65 al cuadrado menos 56 al cuadrado que da 33 cm.
ResponderEliminarPerímetro=2x56+2x33=178cm.
Área=b por h=56x33=1848 cm2
B)Apotema=raíz de 4 al cuadrado menos 2 al cuadrado=3,46 cm
Perímetro=6x4=24 cm
Área=p por a partido entre dos=24x3,46 entre dos=41,52 cm2
C) lado=raíz cuadrada de 5 al cuadrado más 3 al cuadrado=5,83cm
Perímetro=5,83x2+6+12=29,66 cm
Área=B+b entre dos por h =12-6 entre dos por 5=45 cm2
D) Se divide la figura en un cuadrado y un triangulo equilátero, los dos de lado 3 cm.
Triángulo=bxh :2=3x raíz cuadrada de 3 al cuadrado-1,5 al cuadrado entre 2=3,9 cm2.
Cuadrado es A=L al cuadrado-3 al cuadrado=9 cm2.
Figura completa:
Perímetro=5x3=15 cm.
Área=3+3,9=12,9 cm2
Ejercicio 57, pág 167
ResponderEliminarAltura rectángulo: /= √60 × 60 - 40 × 40= √2000= 10√20 cm
P= 2×40 + 2×10 √20= 80+20 √20 cm
A= b×h= 40×10 √20= 400 √20 centímetros cuadrados
Soy Cristina tengo que corregir el ej 35
ResponderEliminarLa fórmula del área del rombo es D Por d entre 2
D mayúscula partido 2 = es igual a la raíz cuadrada de l al cuadrado - (d partido 2) al cuadrado
Que esto sería igual a la raíz cuadrada de 13 e lavado a 2 menos 5 elevado a 2 = 24cm = D
Y por último sustituimos en la fórmula el 24
A= 24 por 10 entre 2 = 120cm cuadrados
Dpartido
Soy Pedro y voy a corregir el ejercicio 58.
ResponderEliminar1/2=raíz cuadrada r elevado a 2 menos a elevado a 2=raíz cuadrada de 7727 elevado a 2 menos 7464 elevado a 2=raíz cuadrada de 3995=1998=/=3997 dm
P=3997 × 12=47,97 dm
A=P × a/2=179,03 dm elevado a 2
Actividad 33 página 160.
ResponderEliminarPerímetro=5+5+8=18cm
h=√5^2-4^2 =3cm
A=b∙h/2=8∙3/2=12cm^2
Página 167 actividad 60
ResponderEliminarA= 3,14 x 4 x 60/360= 3,14 x 2/3= 2,09 cm^2
Actividad 6
ResponderEliminarX=180(n-2)/n=150=180n-360/n=150n=180n-360=-150n+180n-360=30n-360=
=n=360/30=12
Actividad 60
ResponderEliminarEl área del sector circular es:
A=π⋅r2360⋅α=π⋅4360⋅60=2π3=2,09cm2
Ahora calculamos el área del triángulo equilátero que sobra, sabiendo que la base son 2 cm y calculando la altura por Pitágoras.
h=√22−12=√3cm
Área triángulo:
A=b⋅h2=2⋅√32=√3cm2
El área pedida es la resta:
A=2,09−√3=0,36 cm2
Antonio Cobos Cabello
ResponderEliminarEjercicio nº5
La suma de los ángulos de u polígono es 1620º¿Cuántos lados tiene un polígono?
a=180º por (n-2) partido "n"
SOLUCION= 1620/180=n-2
9=n-2
9+2=n
11=n
el polígono tiene 11 lados . Es un endecágono
Soy Juan
ResponderEliminar3
A) S=180°(n-2) S= 540°
B) S=180°(n-2) S= 1440°
C) S=180°(n-2) S= 3240°
Ejercicio 4 de Matemáticas corregido por Carlos Z
ResponderEliminara) 180x(5-2): 5=108°
b) 180x(6-2): 6=120°
c) 180x(10-2): 10=144°
Soy María voy a corregir la actividad 25
ResponderEliminara2 = b2 + c2 => (u2 + v2/2)2 =>(u * v)2 + (u2 - v2/2)2 => (u4 + v4 + 2 u2v2 /4) = u2v2 + (u4 + v4 - 2u2v2 /4) => u4 + v4 +2u2v2 + 4u2v2 + u4 + v4 - 2u2v2 => 2u2v2 = 4u2v2 - 2u2v2 => 2u2v2 = 2u2v2
Se cumple la igualdad por lo qu es un triéngulo recténgulo.
Es necesaria la condición inicial para saber que la longitud de c sea un número positivo y no negativo.
Ejercicio 1 pág 153
ResponderEliminarCuadrado, Pentágono, triángulo isosceles, cuadrilátero y trapecio rectángulo