El periodo de una función


Una gráfica es periódica si su dibujo se repite eternamente y no solo un trozo. En esta gráfica puedes ver que el dibujo se repite, como una ola, pues si miras cada cuanto se repite, esto será su periodo. ¿Desde donde mido? Pues desde cualquier punto hasta que se repite el mismo punto, normalmente se toma un máximo o un mínimo porque es más fácil de delimitar. ¿Qué mido? En el eje x miro que la distancia entre los dos máximos es de cuatro cuadros y como cada dos cuadros es 1 (segun me indica esta gráfica), el periodo será 2. Otra forma: Según lo que marca el dibujo, uno de los máximos está en el punto x=3 y el siguiente está en x=5, por lo que 5-3=2 unidades de medida sería el periodo de esta función. Si hubiera cogido el primer máximo dibujado sería x=1 y el segundo x=3, 3-1=2. Siempre se va a repetir la distancia entre los máximos de esta representación y coincide con el periodo.
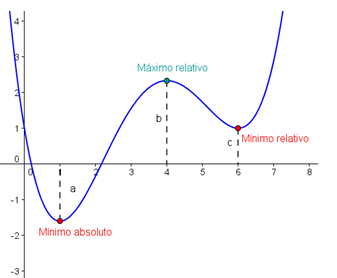
Máximos y mínimos
 Si
Si
 Si
Si

 El dominio son todos los números reales y la imagen es
El dominio son todos los números reales y la imagen es
32
a) Si por cada minuto o fracción a partir de dos minutos se pagan 0,10 €, cuestan lo mismo las dos llamadas. Se pagan los dos minutos iniciales más 3 minutos completos, más la fracción de minuto restante: 0,50 + 3 · 0,10 + 0,10 = 0,90 €.
b)
Máximos y mínimos

Un extremo (máximo o mínimo) es aquel en el que la función aumenta y luego disminuye o al revés. Todos son relativos y el más alto, en el caso de un máximo será el absoluto, de este solo hay uno a no ser que tengas varios a la misma altura.
Así en la gráfica superior en x=1 hay un mínimo absoluto puesto que en la función no hay ningún punto más abajo de él, ningún punto tiene un valor de "y" menor a -1.8.
En x=6 hay un mínimo relativo puesto que el de x=1 es menor.
En cambio, en x=4 hay un máximo relativo (y no absoluto) puesto que la función toma valores superiores al de él (con y>2.5).
Los puntos x=-1 o x=7, no son extremos, puesto que la función tiene que subir y bajar, o al revés.
26
Haz una tabla de valores y representa la función.
 Indica su dominio y su recorrido.
Indica su dominio y su recorrido.

Si




32
a) Si por cada minuto o fracción a partir de dos minutos se pagan 0,10 €, cuestan lo mismo las dos llamadas. Se pagan los dos minutos iniciales más 3 minutos completos, más la fracción de minuto restante: 0,50 + 3 · 0,10 + 0,10 = 0,90 €.
b)
 c) Por las condiciones de la tarifa de la cabina con 0,50 € podemos hablar los dos primeros minutos. Después:, es decir, podemos hablar 5 minutos más. Luego, con 1 € podemos hablar como máximo 7 minutos.
c) Por las condiciones de la tarifa de la cabina con 0,50 € podemos hablar los dos primeros minutos. Después:, es decir, podemos hablar 5 minutos más. Luego, con 1 € podemos hablar como máximo 7 minutos.
d) No es continua. A partir de x = 2, hay un salto cada minuto.
28.
ResponderEliminara) y=10+0,20x
Dependiente y, independiente x
b) x=25
y=10+0,20*25=15
Le cobraron 15€
c) y=52
52=10+0,20x
42=0,20x
x=42/0,20=210
Descargó 210 canciones.
25.
ResponderEliminara) Llamaremos X a la altura, C al cilindro y V al volumen. Entonces, y=2x
TABLA DE VALORES
x 1 2 3 4 5 6
y 2 4 6 8 10 12
b) Llamaremos x al coste, P al producto y B a su beneficio, entonces y=4x
TABLA DE VALORES
x 1 2 3 4 5 6
y 4 8 12 16 20 24
*NOTA: Nos pide también una gráfica pero es imposible representarla mediante ordenador.
23.
ResponderEliminarA) 1,2 Dufi
2,6 Antino
4,4 Biteca
7,6 Colibra
B) Erandio es grande como un orangután y lento como un caracol
C) el conjunto inicial es el tamaño y el final la velocidad
D) no es una función porque un mismo tamaño de superhéroe le corresponden velocidades distintas.
27.
ResponderEliminara)
f(3)= 3 elevado al cuadrado -3(3)+4=4
f(-1)=(-1)elevado al cuadrado-3(-1)+4=8
f(0)=0 al cuadrado-3(0)+4=4
b)
f(x)=-2=x al cuadrado -3x+4=-2 : x al cuadrado -3x+4=-2 :x al cuadrado-3x+6=0
No existe un valor para x tal que f(x)=-2
f(x)=4 = x elevado al cuadrado-3x+4=4 :x al cuadrado -3x+4=4 : x al cuadrado - 3x= 0 : x1 =0, x2 =3
Los valores x1 y x2 cumplen f(0)=4 y f (3)=4
27 f(3)=32−3⋅3+4=4
ResponderEliminarf(−1)=(−1)2−3⋅(−1)+4=8
f(0)=02−3⋅0+4=4
Para f(x)=−2
se resuelve x2−3x+4=−2, entonces, x2−3x+4=−2⇒x2−3x+6=0
Esta ecuación de segundo grado no tiene solución porque el discriminante Δ=(−3)2−4⋅1⋅6=−15<0
No existe un valor para x tal que f(x)=−2
Para f(x)=4
se resuelve x2−3x+4=4, entonces, x2−3x+4=4⇒x2−3x=0⇒x1=0,x2=3
Los valores x1=0,x2=3
cumplen f(0)=4 y f(3)=4.
ACTIVIDAD 42
ResponderEliminar1º:
La variable dependiente es y, que corresponde al número de trabajadores y la variable independiente es x, que corresponde al tiempo que tardarán en levantar el muro.
2º: TABLA DE VALORES:
X: 36, 18, 12,6, 4
Y: 1, 2, 3, 6, 9
3º: REPRESENTACIÓN DE LOS PUNTOS OBTENIDOS.
No se puede representar mediante ordenador.
4º:
No tiene sentido unir los puntos ya que la función no tiene valores intermedios y el número de trabajadores es natural.
EJERCICIO 31
ResponderEliminar3(cuadrado) - 3 x 3 + 2 = (3-1)(3 + a). 2=6 +2a. a= -4/2=-2.
a=-2
34
ResponderEliminara) Sí son periódicas. La función f(x) tiene periodo T = 3 y la función g(x) tiene periodo T = 6.
b)Como 150 = 50 · 3 + 0, entonces f(150) = f(0)= 5,5.
Como 150 = 25 · 6 + 0, entonces g(150) = g(0) = −3.
Ejercicio 48:
ResponderEliminara) El móvil B partió a las 9:30
b) Cada móvil recorre en total 100km/ Móvil A: 5 horas/ Móvil B:4 horas
c) Móvil A:14:00horas/ Móvil B:13:30horas
d)Primero se encuentran a las 11:15 a 35km del punto de partida y después a las 13:00 a
80km del punto de partida
e) A 60km llegará antes el móvil A
A 90km llegará antes el móvil B
A 35km llegará antes el móvil B
f) El móvil A se encuentra a 10km y el móvil B se encuentra a 30km
10
ResponderEliminara)
10kg=1.5g
30kg=4.5g
70kg=10.5g
b)
100kg
C)
D(f)=[o,inf]
R(f)=[0,15]
40-
Función impar=0
Función par= depende de la expresión de la función
44)
ResponderEliminara)En el eje de abscisas se representan las horas del día y en el eje de ordenadas se representa el número de usuarios.
b) Está cerrado desde las tres hasta las cinco de la madrugada.
c)El dominio es [0,24]
d)Sí, es una función continua.
e)Creciente:(5,8)U(10,14)U(17,19)
Decreciente:(0,3)U(8,10)U(14,16)U(19,24)
f)Máximos relativos: x=8, x=14,x=19. x=8 máximo relativo.
Mínimos relativos: x=10. No tiene mínimo relativo
49:
ResponderEliminara) Si x es la altura del triángulo e y su área: y= x(6-x)= -x2+6x
b) El dominio es (0,6)
c) Tabla de valores
X:1,2,3,4,5
Y:5,8,9,8,5
d) El máximo valor del área es 9, se obtiene para x=3
44 Donde dice relativo, quiere decir absoluto.
ResponderEliminar43:
ResponderEliminara) y= 3 + 30x
b) y= 3 + 30 x 25=3 + 750= 753 se pagará 753€
c) 183= 3+3x —> 180= 30x—> x= 180/30= 6
Luis compró 6g de oro.
50.
ResponderEliminara) El perímetro es p(x)= 150 + 2x
b) si llamamos f(x) al área del recinto, entonces f(x)= 150 x x
c) Teniendo en cuenta que la longitud de la valla es como máximo 250 m, el valor de x puede estar entere 0 y 5, por lo que el dominio (o, 50).
d) TABLA DE VALORES
x 0 10 20 30 40 50
f(x) 0 1500 3000 4500 6000 7500
e) Alcanza el máximo pa x= 50 y el área máxima del recinto puede ser 75000 m cuadrados
ACTIVIDAD 13
ResponderEliminara) Es discontinua. Los puntos de discontinuidad son: (0,8) (10,14) (16,24)
b) Discontinua y hay un salto en x = 3.
Ejercicio 54
ResponderEliminarLa respuesta correcta es la D. 0,25, ya que corresponde a los valores:
x: 0´5
y: 0´5
19.
ResponderEliminarDecreciente: (-∞,-15/2)u (0,5)
Creciente: (-15/2,0)u(5,+∞)
Minimo relativo: x=-15/2 y x=5
Máximo relativo: x=0
Actividad 53:
ResponderEliminar10t^2= 10(2,5)^2= 62,5
Respuesta correcta: B.62,5
Ejercicio 34
ResponderEliminara. Son periodicas ya que la funcion f(x) tiene periodo 3 y la funcion g(x) tiene periodo 6.
b. Como 150= 50 x 3 + 0 -- f(150) =f(0)= 5.5
como 150= 25x 6 + 0 -- entonces g(150) =g(0)= -3