Relaciones tróficas de los seres vivos

Niveles troficos

Los organismos de un ecosistema obtienen de distintos modos la materia y la energía que necesitan.

Un nivel trófico está constituido por los organismos que obtienen la materia y la energía de la misma forma.

1. Productores. Son los organismos que producen materia orgánica a partir de materia inorgánica. Los seres vivos autótrofos, fundamentalmente los fotosintéticos (plantas verdes, algas y algunos microorganismos), pertenecen a este nivel trófico.

2. Consumidores primarios. Se alimentan directamente de los productores. Los organismos heterótrofos (los animales herbívoros en los ecosistemas terrestres y los del zooplancton en los acuáticos) pertenecen a este nivel.

3. Consumidores secundarios. Son los organismos que se alimentan de los consumidores primarios. Se trata, por tanto, de animales carnívoros.

4. Consumidores terciarios. Se alimentan de los consumidores secundarios y también se los conoce como superdepredadores.

5. Descomponedores. Este nivel trófico está constituido por las bacterias y los hongos, que se alimentan de los restos orgánicos de todos los organismos (lo cual incluye sus excreciones, desechos o cadáveres). Convierten la materia orgánica en materia inorgánica utilizable por los productores.

Actividades 10, 11, 12 y 13

Cadenas tróficas
Los diferentes niveles tróficos se relacionan entre sí debido a su interdependencia alimentaria.

Los organismos de un nivel trófico pueden vivir porque toman la materia y la energía necesarias del nivel trófico inferior. De este modo se establece una cadena trófica o de alimentación en la que cada grupo se alimenta del anterior y sirve de alimento al siguiente.

Una cadena trófica es una representación unidireccional de la transferencia de materia y energía de unos organismos a otros.

energía de la misma forma.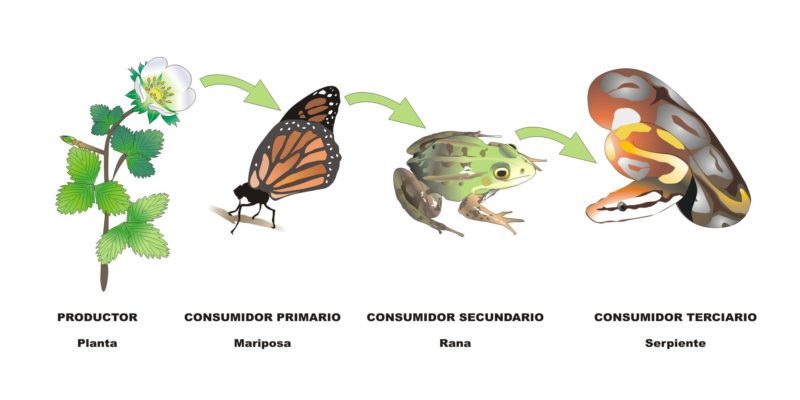
Cadenas Tróficas: Concepto, Tipos, Características y Ejemplos

En una cadena trófica participa un número reducido de organismos debido a las pérdidas de energía que se producen en el paso de un eslabón a otro. La mayoría de las cadenas tienen tres, cuatro o cinco eslabones, aunque en los ecosistemas acuáticos pueden ser más largas.

Generalmente las cadenas tróficas se inician con un productor que es consumido por un herbívoro, y se denominan cadenas tróficas de los herbívoros.

Redes tróficas

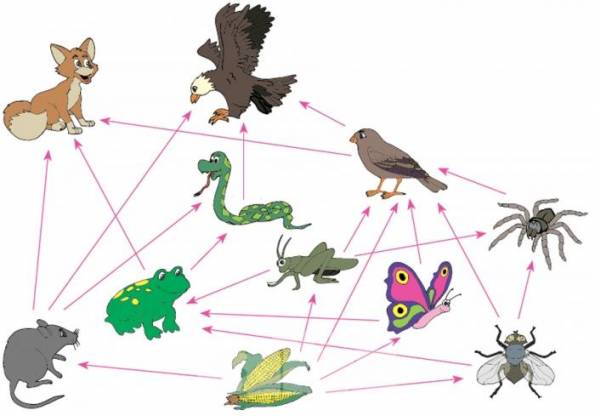
Sin embargo, las cadenas tróficas no tienen lugar de un modo aislado, sino que están interrelacionadas: una especie puede alimentarse de otras pertenecientes a diferentes cadenas y, a su vez, servir de alimento a distintas especies. Por este motivo, en la naturaleza, más que cadenas, existen redes tróficas.

Definición de Red trófica - Qué es y Concepto

Actividades 14, 15, 16, 17

Pirámides tróficas

Las pirámides tróficas o pirámides ecológicas son una forma de representar los diversos niveles tróficos de un ecosistema. Están constituidas por una superposición de rectángulos cuya base es proporcional a los valores que representan (energía, biomasa o número de individuos). Cada rectángulo corresponde a un nivel trófico. En la base de estas pirámides se sitúan los productores y, sobre ellos, los consumidores. Los descomponedores no figuran en ellas, ya que, al alimentarse de todo tipo de restos orgánicos, no constituyen un nivel trófico.

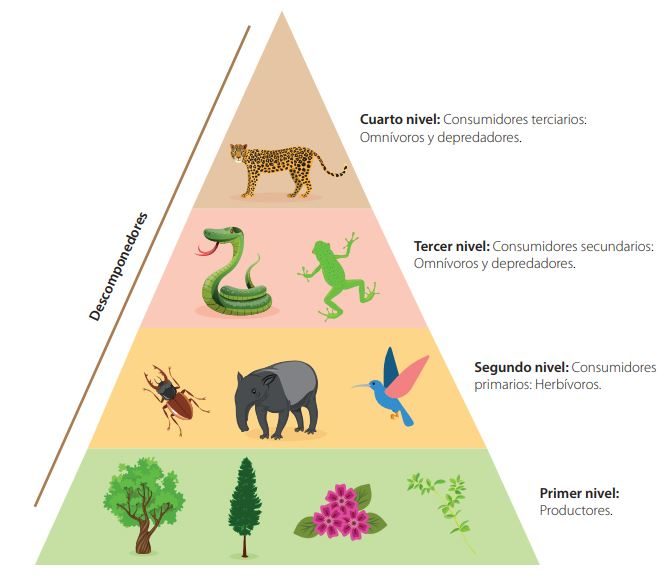
Pirámide trófica o ecológicas y tipos; de energía, de biomasa y ...

Tipos de piramides tróficas:

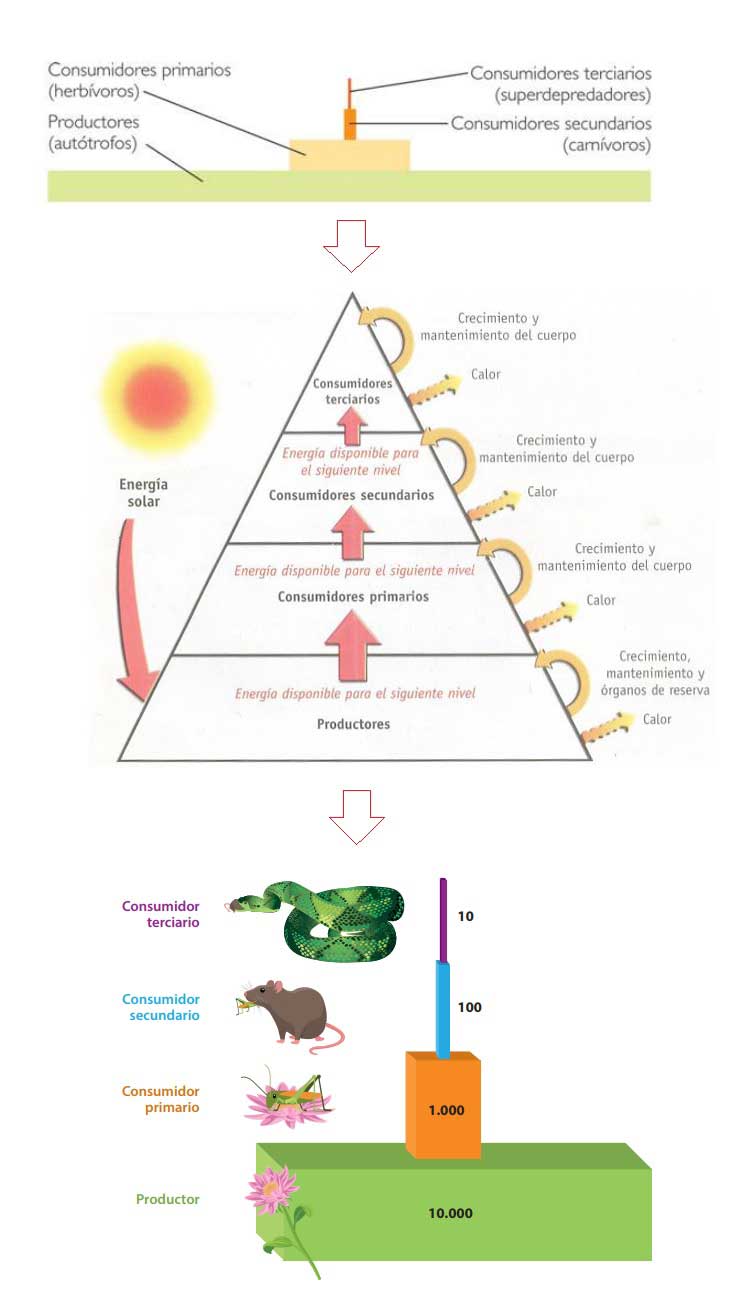
Pirámides de energía. Representan la energía almacenada en cada nivel trófico.

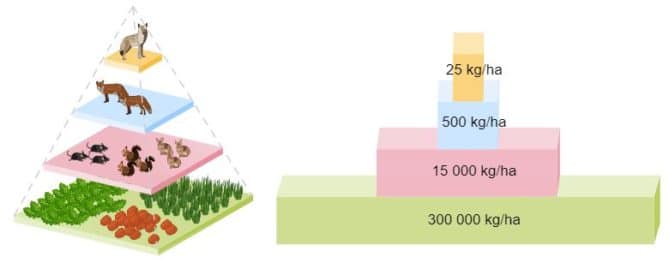
Pirámides de biomasa. Representan la cantidad de biomasa existente en cada nivel trófico.

Pirámides de números. Representan el número de individuos de cada nivel trófico.

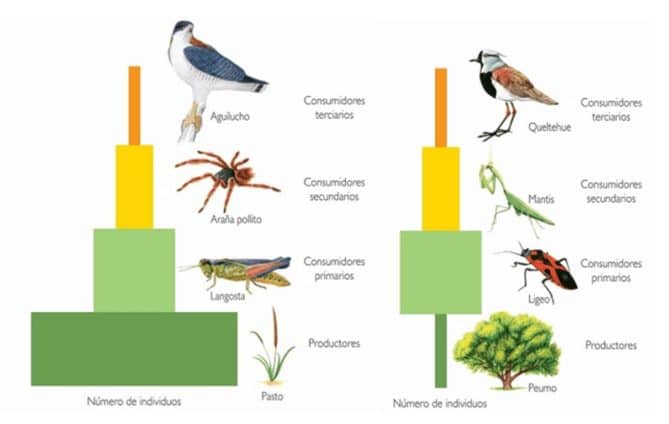
Las pirámides de números y de biomasa pueden estar invertidas, es decir, el nivel de los productores ser menor que el de los consumidores primarios. Esto ocurre cuando unos pocos individuos de gran tamaño sirven de alimento a muchos de pequeño tamaño, o cuando la tasa de reproducción de los productores es muy alta.

Actividad 23 y 24

Las funciones lineales

Las funciones lineales son de la forma y = mx + n, donde m y n son números reales cualesquiera.

La gráfica de cualquier función lineal es una recta.
El número m es la pendiente de la recta.
El número n se llama ordenada en el origen.

Pendiente de una recta

La pendiente mide la inclinación de la recta. El signo de la pendiente indica cómo varía la variable y, cuando la variable x aumenta.

La recta es creciente, y aumenta.

m > 0

La recta es decreciente, y disminuye.

m < 0

La recta es constante, y no aumenta ni disminuye.

m = 0

Cálculo de la pendiente de una recta a partir de una gráfica:

Dados dos puntos cualesquiera de una recta P(x1,            y1), Q(x2, y2), la            pendiente se define como el cociente m=y2−y1/x2−x1

En el MRU, la pendiente de la recta corresponde a la velocidad, ya que en el eje "y" está el desplazamiento, y en el eje "x" está el tiempo. La velocidad es desplazamiento entre tiempo. Entonces, m=v y n=s0, por lo que la ordenada en el origen será la posición inicial. Fijaros en la similitud:
y = mx + n
S = vt + So
Se representan x e y, en física representamos t y s. La pendiente es m y en física, será la velocidad. La ordenada en el origen n, será S0. Es complicado al principio, pero luego se comprende.

Función de proporcionalidad directa

Si la ordenada en el origen es nula, n = 0, la función lineal es y = mx. Las funciones y = mx se llaman funciones de proporcionalidad directa.

La pendiente m ≠ 0 se llama constante de proporcionalidad.

Su gráfica es una recta que pasa por el origen.

Función constante
Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Actividad 1, 2, 3, 4, 5, 6 y 7

Ecuaciones de la recta

Vamos a ver diferentes formas de expresar la misma información. Se pueden transformar unas en otras aplicando operaciones.

1. Ecuación explícita (despejamos la y)

Una recta de la forma y = mx + n, donde m es la          pendiente y n es la ordenada en el origen (punto de corte con el eje y), está expresada en forma            explícita.

La ecuación explícita de una recta se puede calcular conociendo dos de sus puntos.

Ejemplo: Halla la ecuación de la recta que pasa por A(−1, −1) y B(2, 3)
Como A y B son puntos de la recta, sus coordenadas deben cumplir la ecuación, es decir, al sustituir las coordenadas en la ecuación y = mx + n se obtiene:(Recordamos que el primer valor, en las coordenadas de un punto, es de "x" y el segundo de "y")

$\begin{array}{l} - 1 = m \cdot (- 1) + n \\ 3 = m \cdot (2) + n \end{array}} \Rightarrow \begin{array}{l} - 1 = - m + n \\ 3 = 2 m + n \end{array}} \Rightarrow - 1 + m = 3 - 2 m \Rightarrow m = \frac{4}{3} y n = \frac{1}{3}$
$\begin{array}{l} - 1 = m \cdot (- 1) + n \\ 3 = m \cdot (2) + n \end{array}} \Rightarrow \begin{array}{l} - 1 = - m + n \\ 3 = 2 m + n \end{array}} \Rightarrow - 1 + m = 3 - 2 m \Rightarrow m = \frac{4}{3} y n = \frac{1}{3}$
$\begin{array}{l} - 1 = m \cdot (- 1) + n \\ 3 = m \cdot (2) + n \end{array}} \Rightarrow \begin{array}{l} - 1 = - m + n \\ 3 = 2 m + n \end{array}} \Rightarrow - 1 + m = 3 - 2 m \Rightarrow m = \frac{4}{3} y n = \frac{1}{3}$
$\begin{array}{l} - 1 = m \cdot (- 1) + n \\ 3 = m \cdot (2) + n \end{array}} \Rightarrow \begin{array}{l} - 1 = - m + n \\ 3 = 2 m + n \end{array}} \Rightarrow - 1 + m = 3 - 2 m \Rightarrow m = \frac{4}{3} y n = \frac{1}{3}$
La ecuación de la recta es $y = \frac{4}{3} x + \frac{1}{3}$
.
La ecuación explícita de una recta se puede calcular conociendo uno de sus puntos y la pendiente.

Ejemplo: Calcula la ecuación explícita de la recta cuya pendiente es m = 3 y que pasa por el punto A(2, −4).

Como m = 3, la ecuación de la recta es y = 3x + n.
El punto A(2, −4) pertenece a la recta, por tanto debe verificar su ecuación: (Sustituyo el valor de "x" e "y" del punto que me dan)

−4 = 3 ⋅ 2 + n ⇒ n = −4 − 6 = −10

La ecuación explícita de la recta es y = 3x − 10.

2. Ecuación de la recta que pasa por dos puntos

Si una recta pasa por los puntos P(x1, y1),            Q(x2, y2), su ecuación es: 

                     y−y1/y2−y1=x−x1/x2−x1

Ejemplo: Calcula la ecuación de la recta que pasa por los puntos A(2, −3) y B(1, 5).

\frac{y - (- 3)}{5 - (- 3)} = \frac{x - 2}{1 - 2} \Rightarrow \frac{y + 3}{8} = \frac{x - 2}{- 1}

3. Ecuación punto-pendiente

Si una recta tiene una pendiente m y pasa por el punto            P(x1, y1), su ecuación es: 

                              y − y1 = m(x −            x1)

Ejemplo: Halla la ecuación punto-pendiente de una recta con pendiente m = −2 y que pasa por el punto A(0, 2). Exprésala en forma explícita.

Se sustituye la pendiente y las coordenadas del punto en la ecuación:

y − 2 = −2(x − 0) ⇒ y − 2 = −2x

Para hallar la forma explícita, despejamos y: y = −2x + 2

Observa que, como

m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

, se cumple:

m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}

\frac{y - y_{1}}{y_{2} - y_{1}} = \frac{x - x_{1}}{x_{2} - x_{1}} \Rightarrow y - y_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (x - x_{1})

Es decir, y − y₁ = m(x − x₁). Podemos pasar fácilmente de la ecuación de recta que pasa por dos puntos a la ecuación punto - pendiente. Y de aquí despejando "y" obtendriamos la ecuación explícita.

4. Ecuación general o implícita (todo a un miembro e igualamos a 0)

Una recta de la forma ax + by + c = 0 está escrita en forma general o implícita.

Ejemplo: Expresa la recta $y = \frac{1}{3} x + \frac{1}{6}$ en forma general.

y = \frac{1}{3} x + \frac{1}{6} \Rightarrow \frac{6 y}{6} = \frac{2 x}{6} + \frac{1}{6} \Rightarrow 6 y = 2 x + 1 \Rightarrow - 2 x + 6 y - 1 = 0

Actividades 9, 11, 12, 13, 14, 15, 17, 18

Física y Química

La meteorología es parte de la física

jueves, 30 de abril de 2020

Relaciones tróficas de los seres vivos

Las funciones lineales

Pendiente de una recta

Función constante
Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Actividad 1, 2, 3, 4, 5, 6 y 7

Función constante
Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Actividad 1, 2, 3, 4, 5, 6 y 7

Ecuaciones de la recta

1. Ecuación explícita (despejamos la y)

Ejemplo: Calcula la ecuación explícita de la recta cuya pendiente es m = 3 y que pasa por el punto A(2, −4).

2. Ecuación de la recta que pasa por dos puntos

Ejemplo: Calcula la ecuación de la recta que pasa por los puntos A(2, −3) y B(1, 5).

3. Ecuación punto-pendiente

Ejemplo: Halla la ecuación punto-pendiente de una recta con pendiente m = −2 y que pasa por el punto A(0, 2). Exprésala en forma explícita.

4. Ecuación general o implícita (todo a un miembro e igualamos a 0)

Ejemplo: Expresa la recta $y = \frac{1}{3} x + \frac{1}{6}$ en forma general.

Archivo del blog

Prensa

La meteorología es parte de la física

jueves, 30 de abril de 2020

Relaciones tróficas de los seres vivos

Las funciones lineales

Pendiente de una recta

Función constante Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X. Actividad 1, 2, 3, 4, 5, 6 y 7

Función constante Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Actividad 1, 2, 3, 4, 5, 6 y 7

Ecuaciones de la recta

1. Ecuación explícita (despejamos la y)

Ejemplo: Calcula la ecuación explícita de la recta cuya pendiente es m = 3 y que pasa por el punto A(2, −4).

2. Ecuación de la recta que pasa por dos puntos

Ejemplo: Calcula la ecuación de la recta que pasa por los puntos A(2, −3) y B(1, 5).

3. Ecuación punto-pendiente

Ejemplo: Halla la ecuación punto-pendiente de una recta con pendiente m = −2 y que pasa por el punto A(0, 2). Exprésala en forma explícita.

4. Ecuación general o implícita (todo a un miembro e igualamos a 0)

Ejemplo: Expresa la recta y=1/3x+1/6en forma general.

Función constante
Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Actividad 1, 2, 3, 4, 5, 6 y 7

Función constante
Si la pendiente es nula, m = 0, la función lineal es y = n. Las funciones y = n se llaman funciones constantes. Como m = 0, la función no es creciente ni decreciente. Su gráfica es una recta paralela al eje X.

Ejemplo: Expresa la recta $y = \frac{1}{3} x + \frac{1}{6}$ en forma general.